Today I Learned (TIL): Algorithm Patterns
Like many aspiring software engineers, I've been practicing data structures and algorithms in hopes of "cracking the coding interview".
From hacking on so many problems using platforms like BinarySearch and AlgoExpert, I've come to a point where I want to document common patterns. With these patterns, I'm hoping to build a better mental model so that I can solve problems faster.
Pattern 1: Sliding Window
Code sniff
- Problems dealing with linear data structures like Array or LinkedList or String
- Find contiguous subarrays or sublists of a given size
Example
- Given an array, find the average of all contiguous subarrays of size "K" in it
Strategy
Brute Force
- For every element of the input, find the next k elements.
- Time Complexity: O(N * K)
- Inefficiency: Recalculating/traversing overlapped portion
Can we do better?
Sliding Window Approach
- Visualize each contiguous subarray as a sliding window of size K.
- We slide window by one element when we move on to the next subarray.
- To re-use the sum from previous subarray, we subtract the element going out of window and add element now being included in sliding window.
- If our window is dynamic, have an internal while loop to shrink window until we hit the desired length
- Time Complexity: O(N)
- Initialize:
windowStart = 0andwindowEnd = iterator in for loop - Slide window:
accumulator -= arr[windowStart]andwindowStart++
Pattern 2: Merge Intervals
Code sniff
- Problems involving intervals.
- Detect if intervals overlap and merge them
- Produce a list with only mutually exclusive intervals
Strategy
Know the 6 cases that 2 intervals (a, b) can relate to each other:
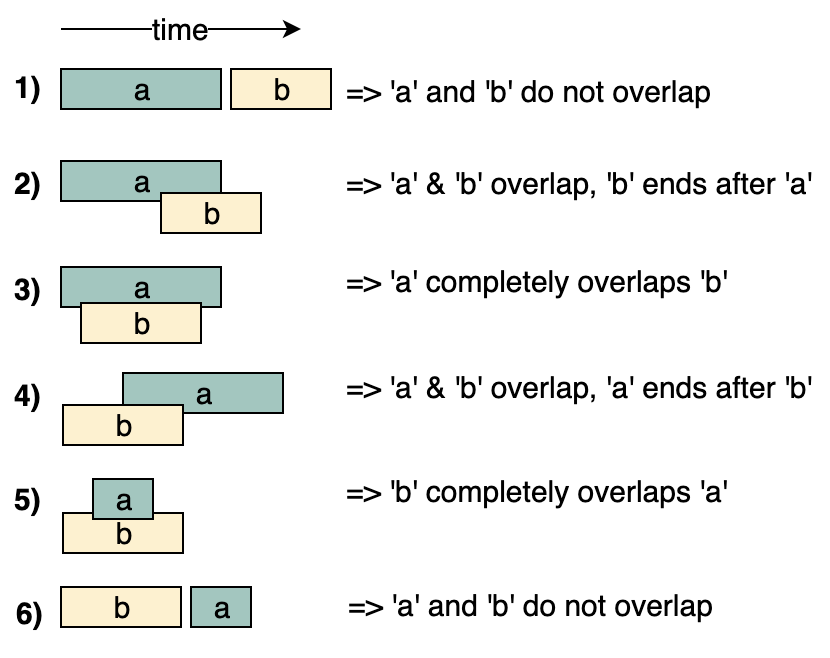
- Case 1 and 6; Case 2 and 4; Case 3 and 5 are complements for each other. You can simplify these cases by sorting intervals in order based on start time.
Code Example
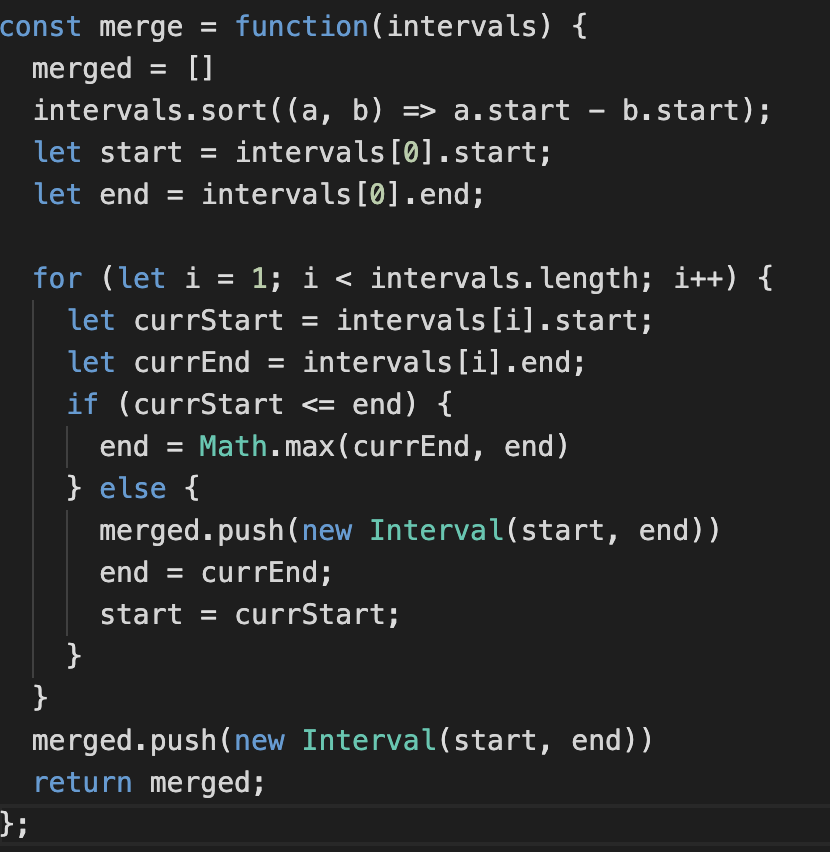
-
- Sort intervals in order based on start time
-
- Initialize start and end with first interval
-
- Loop through all intervals starting from the second one
- Case 1: Overlap: Update end time
- Case 2: No Overlap: Add previous interval + reset
- Avoids while loop
-
- Since we add previous interval, when we reach the end we need to add the last interval.
Pattern 3: Greedy
Code sniff
- Shortest paths in a graph
- Minimum spanning tree
- Huffman codes for data compression
- Clustering
- Interval Scheduling
Strategy
- Solution is built in small steps. A decision is made at each step to optimize for a single criterion
Code Example
-
Interval Scheduling problem: Single resource, many requests with starting and ending time. Find set of max requests you can fill.
-
Rule: Accept request that finishes first
-
- Use a simple rule to select first request
i
- Use a simple rule to select first request
-
- Reject all requests not compatible with
i
- Reject all requests not compatible with
-
Interval Partitioning problem: Many resources, many requests : Find fewest resources to fill all requests
-
Rule: The number of resources needed is at least the depth of the set of intervals.
-
- Sort intervals by start times :
I
- Sort intervals by start times :
-
- Loop through all intervals
- For each interval
I_ithat precedesI_jand overlaps it, exclude label ofI_ifromI_j - if there is any label not excluded, then assign that label to
I_j - else leave
I_junlabeled
-
No overlapping intervals will receive same label. You have d labels, as you sweep through the intervals from left to right, assigning an available label to each interval, you cannot reach a point where all labels are in use
-
Schedule to Minimize Lateness Single resource, multiple requests, different deadline: Minimize overall lateness
-
Rule: Earliest deadline first: Sort jobs in increasing order of deadlines